Description of the key parts of the heuristic.

Flowchart of the heuristic

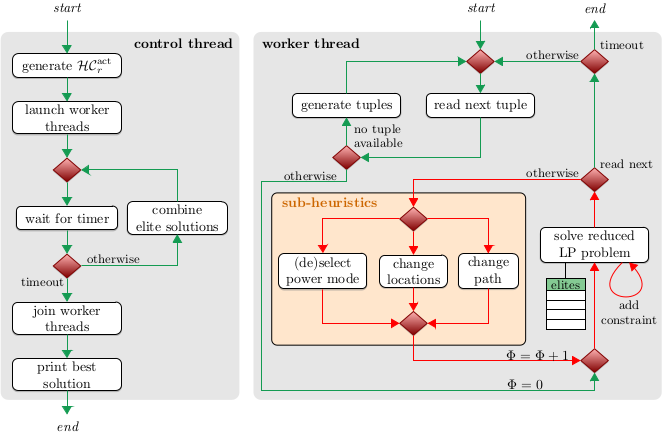
Brief description of the blocks

block	description	reference
generate 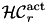$\mathcal{HC}_r^{\mathrm{act}}$	It generates various robot alternatives 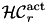$\mathcal{HC}_r^{\mathrm{act}}$ , i.e. Hamiltonian Circuits that visits each static activity just once. An alternative indirectly specifies the order of operations, however, go-through coordinates (called locations) do not have to be known.	ParallelHeuristicSolver::generateRandomAlternatives, ParallelHeuristicSolver::generateShortestCircuits
combine elite solutions	Alternatives used in elite solutions are randomly selected to generate new promising tuples, i.e. partially fixed problems. These tuples should intensify the searching process, and as a result, a better quality of solutions is expected.	ParallelHeuristicSolver::generatePromisingTuples
read next tuple	The next tuple (a partially fixed problem) is read from the knowledge base, i.e. shared data of the heuristic.	KnowledgeBase::getTuple
generate tuples	A candidate tuples, i.e. partially fixed problems, are generated and added to the knowledge base.	ParallelHeuristicSolver::addRandomTuplesToKB, KnowledgeBase
solve reduced LP problem	Given fixed locations, movements, and power saving modes the partially fixed problem is solved to obtain timing of the robotic cell. The resulting timing and the partially fixed problem gives a feasible solution which may be added to the list of elite solutions. Note that it may be necessary that Linear Programming is called more than once to resolve collisions between robots	HeuristicAlgorithms::solvePartialProblem, HeuristicAlgorithms::resolveCollision, HeuristicAlgorithms::resolveTheWorstCollision
(de)select power mode	This sub-heuristic selects a location where an original power saving mode of the robot will be changed to another one to save energy. Estimation of the energy reduction is based on Gantt scaling and on the violation of global time constraints.	HeuristicAlgorithms::heuristicPowerModeSelection, HeuristicAlgorithms::scaleGanttToCycleTime, HeuristicAlgorithms::calculateBreakagePenalty
change locations	This sub-heuristic locally optimizes the robot paths through locations. Basically, for each consecutive triple of locations 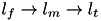$l_f \rightarrow l_m \rightarrow l_t$ , corresponding to a part of the robot closed path, a middle location 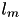may be replaced by another one if it is more energy efficient. Golden Section search method is used to find the best replacements.	HeuristicAlgorithms::heuristicLocationChanges, goldenSearch, UnimodalFunctionHeuristic
change path	This sub-heuristic diversifies the search process by perturbing the robot paths. This moves the heuristic to other parts of the solution space that would be otherwise unreachable.	ParallelHeuristicSolver::changeRobotPaths
optimization part	The goal of the part highlighted by red arrows is to optimize already feasible solutions. The maximal number of optimization iterations without a significant improvement is denoted as 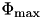$\Phi_{\mathrm{max}}$ .	Settings::MIN_ITERS_PER_TUPLE
control thread	The thread that generates alternatives, launches the worker threads, generates promising tuples from time to time, and joins the worker threads after a given time limit.	ParallelHeuristicSolver::controlThread
worker thread(s)	The main responsibility of worker threads is to generate the tuples and optimize them to find a good quality solutions.	ParallelHeuristicSolver::workerThread, Settings::NUMBER_OF_THREADS

Reduced Linear Programming problem

This part presents a Linear Programming formulation used for solving partially fixed problems. The most of the used symbols and variables is defined in mathematical formulation page, however some additional symbols are required to be set out. 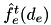$\hat{f}_e^t(d_e)$ is the energy function of dynamic activity 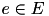$e \in E$ and its movement 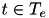$t \in T_e$ . These functions are convex and piece-wise linearized, and therefore appropriate for a tailor-made Gurobi simplex algorithm. Sets 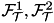$\mathcal{F}_{\!\mathcal{T}}^1, \mathcal{F}_{\!\mathcal{T}}^2$ are extracted from the tuple and determine which movements, locations, and power saving modes are fixed. The constraints marked by asterisks correspond to the ones in the Integer Linear Programming formulation but they are generated from different sets since only a sub-part of the problem is taken into account. And finally, sets 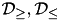$\mathcal{D}_{\geq}, \mathcal{D}_{\leq}$ generate additional constraints that resolve collisions by adding 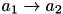$a_1 \rightarrow a_2$ precedence or vice versa. The resulting energy-efficient timing is feasible for the original formulation.

$\begin{alignat*}{3} & \text{minimize} \displaystyle \sum_{\forall (e, t) \in \mathcal{F}_{\!\mathcal{T}}^1} \hat{f}_e^t(d_e) + \sum_{\forall (v,l,m) \in \mathcal{F}_{\!\mathcal{T}}^2} p_{v,l}^m d_v \\[1mm] & \quad \text{subject to:}\;\text{(9)*}, \text{(10)*}, \text{(14)*}, \text{(15)*}, \text{(16)*} \\ & \quad s_{a_2}+ n \mathrm{CT} \geq s_{a_1}+d_{a_1} \qquad \forall (a_1, a_2, n) \in \mathcal{D}_{\geq} & \qquad & (21) \\ & \quad s_{a_2} + d_{a_2} + n \mathrm{CT} \leq s_{a_1} \qquad \forall (a_1, a_2, n) \in \mathcal{D}_{\leq} & \qquad & (22) \end{alignat*}$

See also: HeuristicAlgorithms::solvePartialProblem, RoboticLineSolverLP, ILPModel