Energy optimization problem of robotic cells formulated as an Integer Linear Programming problem.
General description
Although the energy optimization problem of robotic cells is inherently non-linear, it is possible to formulate it as an Integer Linear Programming problem if the non-linear convex functions are piece-wise linearized. These functions correspond to energy functions of robot movements which express the dependency of the energy consumption on the duration of the movement for a fixed trajectory. A solution for one robot can be perceived as the most energy efficient closed path through the specified stop coordinates, called locations. During the waiting in a stationary robot position a power saving mode of a robot can be applied. If the whole robotic cell is optimized, time synchronizations and the spatial compatibility have to be met, i.e. a workpiece is handed over from one robot to another at the right place at the right time. Finally, as robots are close to each other, the collisions have to be avoided.
Table of used symbols
| symbol | description | reference | type |
|---|---|---|---|
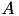 | set of all activities, i.e. 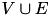 | Activity | set |
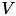 | set of all static activities | StaticActivity | set |
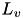 | set of possible coordinates, i.e. locations, for activity  | Location | set |
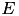 | set of all dynamic activities | DynamicActivity | set |
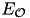 | set of all optional dynamic activities | DynamicActivity | set |
 | set of movements of activity 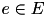 | Movement | set |
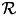 | set of robots | Robot | set |
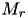 | power saving modes of robot 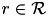 | RobotPowerMode | set |
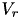 | static activities of robot 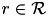 | – | set |
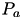 | predecessors of activity 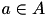 | Activity::mPredecessors | set |
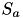 | successors of activity 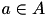 | Activity::mSuccessors | set |
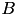 | indices of the piece-wise linear functions | – | set |
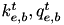 | coefficients of b-th linear function | – | constants |
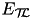 | time lags for inter-robot time synchronization | TimeLag | set |
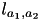 | length of a time lag 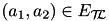 | TimeLag::mLength | constant |
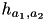 | height of a time lag 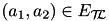 | TimeLag::mHeight | constant |
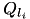 | set of locations compatible with location 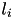 | – | set |
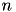 | multiple of the robot cycle time | – | constant |
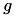 | either movement  or location or location 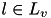 | ActivityMode | mode |
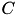 | set of possible collisions | RoboticLine::mCollisions | set |
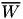 | upper bound on energy consumption | – | constant |
 | static activity that closes the cycle of robot 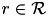 | Activity::mLastInCycle | activity |
 | input power of robot 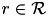 for activity for activity 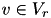 and location and location 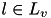 | LocationDependentPowerConsumption | constant |
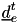 | minimal duration of the movement 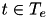 | Movement::mMinDuration | constant |
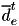 | maximal duration of the movement 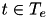 | Movement::mMaxDuration | constant |
Table of variables
| variable | description | reference | type |
|---|---|---|---|
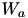 | energy consumption of activity 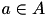 | VariableMappingLP::W | positive float |
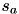 | start time of activity 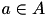 | VariableMappingLP::s | positive float |
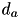 | duration of activity 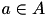 | VariableMappingLP::d | positive float |
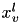 | true if location 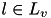 of activity of activity  is selected, otherwise false is selected, otherwise false | VariableMappingILP::x | binary |
 | true if mode 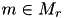 is applied in activity is applied in activity 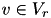 , otherwise false , otherwise false | VariableMappingILP::z | binary |
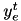 | true if movement 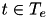 of activity of activity 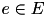 is selected, otherwise false is selected, otherwise false | VariableMappingILP::y | binary |
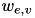 | true if activity 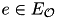 is performed is performed  , otherwise false , otherwise false | VariableMappingILP::w | binary |
 | decides whether  or or 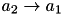 to resolve a collision to resolve a collision | VariableMappingILP::c | binary |
Integer Linear Programming model
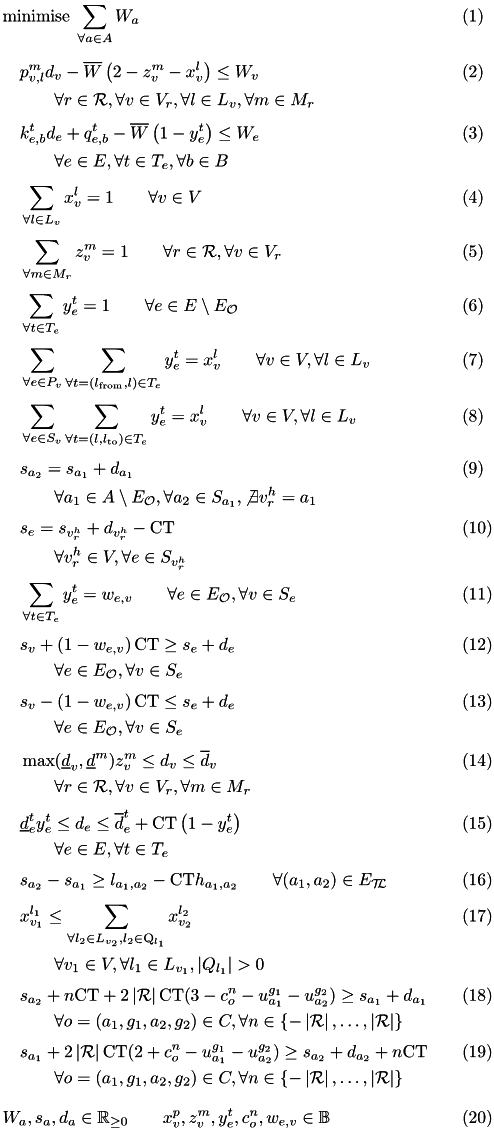
Description of constraints
| constraint(s) | description | reference |
|---|---|---|
| (1) | Minimization of the total energy consumed by all the activities. | RoboticLineSolverILP::construct |
| (2) | Propagation of the energy consumption of static activities to the criterion with respect to the selected locations, power saving modes of robots, and durations. | ConstraintsGenerator::addEnergyFunctions1 |
| (3) | Propagation of the energy consumption of dynamic activities to the criterion with respect to the selected movements and robot speeds. | ConstraintsGenerator::addEnergyFunctions2 |
| (4), (5), (6) | Only one power saving mode and location is assigned to each static activity, and each mandatory dynamic activity has assigned just one movement. Constraints (6) can be omitted as flow preservation constraints (7), (8) and the timing enforce the implicit selection. | ConstraintsGenerator::addUniqueModeSelection |
| (7), (8) | Flow preservation constraints ensure that if the robot enters to a location it also has to leave the same location. | ConstraintsGenerator::addFlowConstraints |
| (9), (10) | Ensure a correct timing for fixed precedences of activities | ConstraintsGenerator::addFixedPrecedences |
| (11), (12), (13) | Ensure a correct timing of optional precedences that model alternative orders of operations. | ConstraintsGenerator::addPrecedenceSelectionConstraints, ConstraintsGenerator::addSelectablePrecedences |
| (14), (15) | Restrictions on durations of static and dynamic activities, respectively. | ConstraintsGenerator::addDurationConstraints |
| (16) | Time synchronization between robots is ensured by time lags. | ConstraintsGenerator::addTimeLags |
| (17) | Constraints enforcing the spatial compatibility for handover operations. | ConstraintsGenerator::addSpatialCompatibilityConstraints |
| (18), (19) | Constraints ensure that two related activities are time disjunctive for different multiples of the production cycle time, and therefore, the collision is resolved. | ConstraintsGenerator::addCollisions |
| (20) | Domain of variables, all the variables of the model are either positive floats or binary variables. | VariableMappingILP |
- Remarks
- In the implementation, constraints (6) are omitted, and some of constraints are merged, therefore the number related to a constraint (in the constraint description) differs from the numbers presented here. This mathematical formulation was adapted to ease the understanding and reading.
 1.8.9.1
1.8.9.1